从原子排列的结构形式来看，固态物 质可划分为晶体、非晶体和准晶体三种。其 中，非晶体不具有长程有序结构，致使人们 无法用精确的数学表达来描述非晶的原子结 构，进而无从理解非晶转变过程中粘度急剧 增大 ( 力学性质从液体变为固体)的根本原 因，严重阻碍了人类对非晶形成物理本质的 认识。该问题也成为了世界公认的科学难题。 物质从液态转变为非晶态要经历一个重要的 转变阶段，即所谓的玻璃化转变。玻璃化转 变的本质是纯动态的还是热力学转变，是凝 聚态物理的一个难题和争论热点。许多研究 试图寻找结构—动力学关联性，以支持玻璃 化转变的热力学现象的观点， 主要包括： (1) 某种局域结构(如球形粒子系统的局部多面 体)与动力学量之间的空间相关性； (2) 随动力学变慢而增长的静态空间尺度。然而， 这两种方法都缺乏定量表征和理论依据。

　　问题的关键在于人们一直囿于一种固定 的思维模式，即非晶具有短程有序结构，而 不具有长程有序结构。所以一直试图通过构 筑短程有序结构基元，并通过研究结构基元 在中程范围内的空间扩展及其与动力学量空 间耦合，揭示玻璃态转变过程及其与热力学 的关联性。然而这导致了两个严重问题：过于分散多样的短程有序结构基元，及缺乏理 论依据和验证。创新既是对原有思维的突破， 而突破需要建立在对所研究对象的本质进一 步凝练和提取上。用直白的语言讲，既是劲 量抛弃非共性的、非本质的东西，保留最基 本的、不可或缺的部分。对于玻璃态转变来 讲，所谓短程有序结构基元并不是必须的， 玻璃态转变并非一定是基于某种有序结构基 元的演变而发生的。实质上需要寻找的是： 局域结构的演变与热力学性能转变之间的联 系。核心关键词两个：局域结构和性能转变。 它山之石可以攻玉。科研上，一个很好的研 究思路是借助其它领域的原理、机制，通过 相似类比，解决本领域里的核心问题。难点 在于如何找到这块石头！伊辛模型(Ising model)是物理学上一个著名理论模型，用 来描述物质相变的随机过程。物质经过相变， 要出现新的结构和物性。发生相变的系统一 般是在分子之间有较强相互作用的系统，又 称合作系统。1920 年，德国物理学家威廉 ·楞 次(Wilhelm Lenz)提出了伊辛模型，用来 描述铁磁性物质内部的原子自旋状态及其与 宏观磁矩的关系。其核心是研究磁畴之间的 相互作用及对宏观磁学性能的影响。单个磁 畴的边界形状是不规则的，磁畴的尺寸分布也具有一定的随机性，结构上可以用结构序 参量来统计性的描述。这启发了我们从实验 上构筑类伊辛模型系统来研究玻璃态转变问 题。我们采用椭球单层胶体球体系，类比二 维伊辛模型系统，研究其玻璃态转变过程。 该系统不存在球形粒子系统中的局部有序结 构或其他多面体结构，具有优异的玻璃形成 能力，提供了研究玻璃化转变的临界行为和 结构动力学相关性的更加普适的条件。

　　通过与香港科技大学合作，首次探索了 非球形粒子玻璃化转变的临界行为，该工作 发表于 Science Advances 杂志 2021 年 1 月 15 日期刊。通过实验和模拟研究，不仅观察 到理想玻璃化转变点 0 的类伊辛临界行为， 还观察到模式耦合转变点 C 的非伊辛临界行 为。伊辛临界存在于静态结构(局域最稳结 构和局部结构熵) 和动态量(缓慢移动粒子) ， 对应一种热力学转变；非伊辛临界性只存在

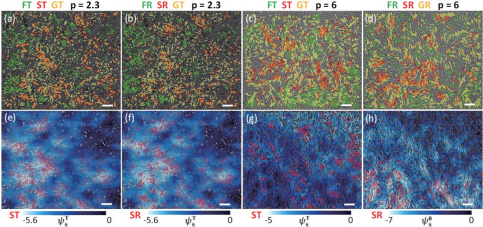
　　图 1：快速(F)、慢速(S)团簇、局域稳态结构(G)和结构熵的空间关联(T：平移，R，θ：转动)。 长径比 p=2.3 粒子：ST 和 SR 团簇都与 GT团簇和低区域正关联；p=6.0 粒子：ST、SR 团簇分别与 GT 团簇和低区域、GR 团簇和低区域正关联，且平移和转动负相关。比例尺：20μm。

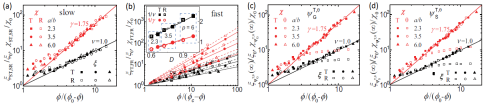
　　图 2：动态协同弛豫和静态结构的类临界行为。(a) 慢速团簇、(b) 快速团簇、(c) 玻璃序参数和 (d) 局部结构熵的平均尺度 ξ 和涨落 χ，分别折叠在两条拟合函数 and 。对于慢速团簇和静态结构量，ν=1 和 γ=1.75 对应于二维伊辛普适性类。(b) 插图：快速团簇的 1/ν 和 1/γ 随脆性指数 D 线性增加。

　　于快速运动粒子的动态量，对应一种动态转 变。研究表明不同长径比的椭球体及平动和 转动自由度，都具有相同的规律。这种非球 形玻璃化系统的伊辛临界行为可根据 P W Anderson 的 two-state model 定性解释。

　　该工作对玻璃化转变的其他热点问题进 行了研究： (1) 寻找动态不均性的结构起源 是玻璃化研究的一个主要方向。该研究发现 低结构熵很好地对应于慢速弛豫运动，且广 泛适用于球体或非球体组成的系统。而文献 中常用的局部结构(如各种多面体)只存在 于某些球体系统中。(2) 以往研究发现玻璃 转变过程中，动力学量发散于 C 或 0，导致 “动力学关联长度如何在两个不同温度下发 散？” 的问题。该研究表明， 基于快速粒子 的动力学量都在 C 发散，基于慢速粒子的动 力学量都在 0 发散。这种基于两种不同时间 尺度的动态量，提供了玻璃化动力学的更全 面的描述。(3)Fragility 是玻璃化系统的 重要性质，该研究发现，具有更强各向异性 的粒子，会降低玻璃化系统的 fragility，与 球形粒子相比，显著提高玻璃形成能力。

　　通过这个科研实例，从中得到了些许点 滴体会，在此与力学所同仁共勉。一是科研 需要保持连续性和持久性。科研工作没有捷 径可寻，对个体而言，也很难实现跨越性发 展。只有坚持不懈，持之以恒，方能对所研 究对象与问题有深入的理解。只有在深入理 解基础上， 才能领悟问题的实质， 抽丝剥茧，深入核心。二是科研需要保持对知识的渴望 和相关领域问题的广泛猎取。扩大了知识面， 并能从中抽取出核心思想和解决问题的路 径，才能触类旁通，找到他山之石，解决自 己的问题。

　　王育人，研究员，中国 科学院微重力重点实验室。 研究领域：1)胶体自组装现 象及新型材料研究；2)空间 复杂流体研究；3)水下声学 材料及声学超材料研究。

　　郑中玉，副研究员，中 国科学院微重力重点实验室。 研究领域：1)软物质统计物 理，2) 复杂流体相变与流变， 3)空间微重力科学。